20种复杂难预测函数时间序列数据集介绍

引言与背景

时间序列预测是机器学习领域中的重要研究方向，在金融市场分析、天气预报、交通流量预测、电力负荷预测等众多领域都有广泛应用。然而，实际应用中遇到的时间序列往往具有高度复杂性，传统的时间序列预测方法在面对混沌系统、非线性过程和随机噪声时常常表现不佳。本数据集旨在为研究人员和工程师提供一个全面的测试平台，用于开发和评估更先进的时间序列预测模型。

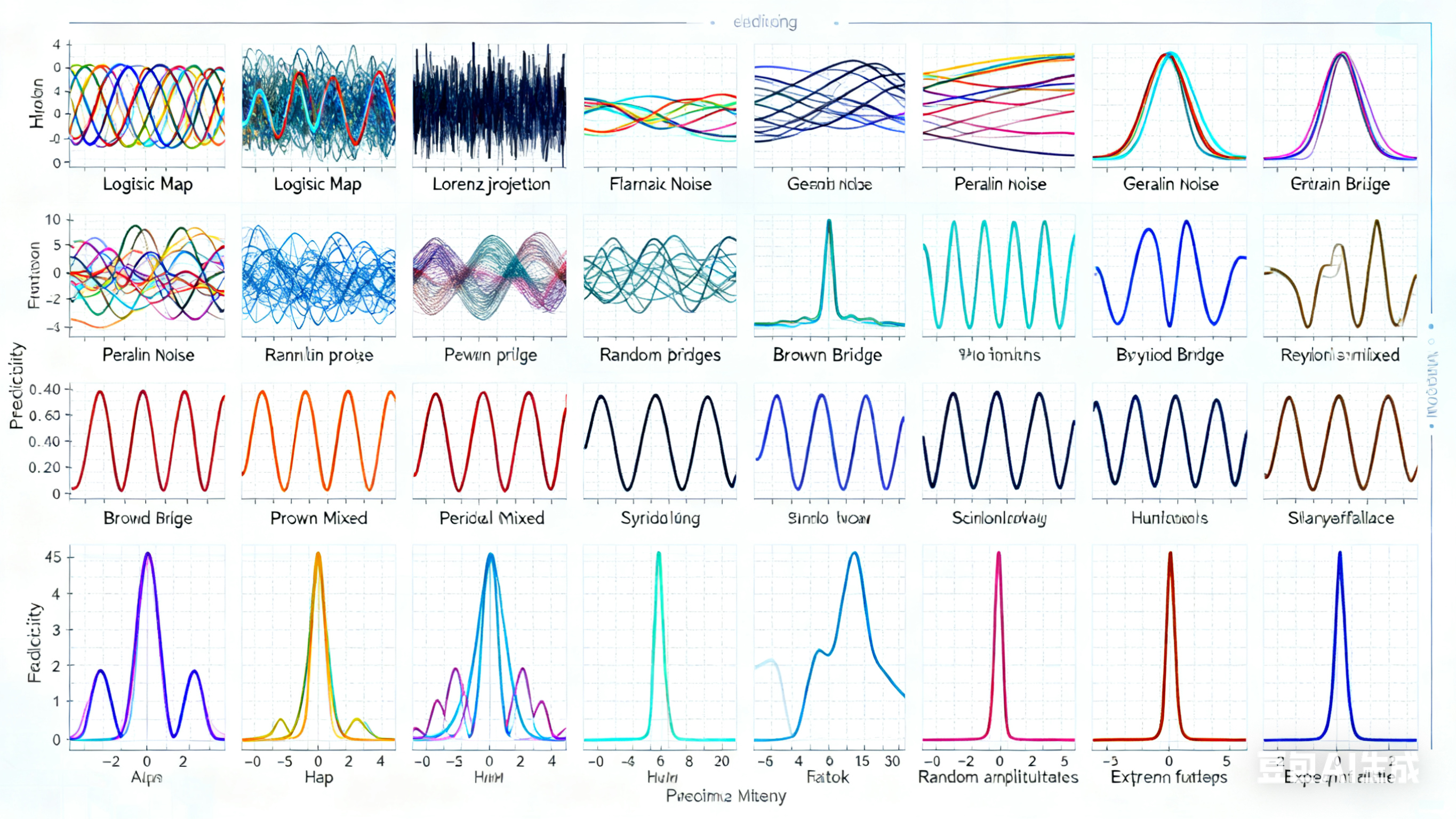
本数据集包含20种不同类型的复杂难预测函数时间序列数据，总计超过1600万条记录。这些数据涵盖了混沌系统、分形噪声、随机过程等多种复杂模式，为机器学习模型的训练和评估提供了丰富多样的测试场景。通过使用这些真实生成的复杂时间序列数据，研究人员可以更好地验证模型在处理非线性、非平稳、混沌和随机过程时的性能表现。

数据基本信息

数据字段说明

字段名称	字段类型	字段含义	数据示例	完整性
X	浮点数	时间步长	0.00, 0.01, 0.02	100%（无缺失）
Y	浮点数	时间序列值	0.00000, 0.00037, 0.00074	100%（无缺失）

数据分布情况

文件数量与记录数分布

文件名称	记录数量	占比	累计占比
henon_like.csv	800,001	5.00%	5.00%
random_amplitude_sine.csv	800,001	5.00%	10.00%
random_sawtooth.csv	800,001	5.00%	15.00%
brownian_bridge.csv	800,001	5.00%	20.00%
gaussian_bumps.csv	800,001	5.00%	25.00%
double_logistic_map.csv	800,001	5.00%	30.00%
random_sine_exponential.csv	800,001	5.00%	35.00%
perlin_noise.csv	800,001	5.00%	40.00%
polynomial_random_bump.csv	800,001	5.00%	45.00%
sum_of_two_sines.csv	800,001	5.00%	50.00%
piecewise_chaotic.csv	800,001	5.00%	55.00%
random_exponential_decay.csv	800,001	5.00%	60.00%
triangle_wave_sign_flips.csv	800,001	5.00%	65.00%
weird_sin_x2.csv	800,001	5.00%	70.00%
spiky_function.csv	800,001	5.00%	75.00%
logistic_map.csv	800,001	5.00%	80.00%
lorenz_x_projection.csv	800,001	5.00%	85.00%
random_walk.csv	800,001	5.00%	90.00%
fractal_noise.csv	800,001	5.00%	95.00%
iterated_polynomial.csv	800,001	5.00%	100.00%

数据类型分布

数据类型	文件数量	占比	特征描述
混沌系统	5	25.00%	高度敏感、确定性但长期不可预测
噪声过程	3	15.00%	随机波动、无明显模式
随机过程	2	10.00%	随机步长、累积效应
复杂周期函数	10	50.00%	含噪声或变形的周期性变化

数据规模与格式

• 总文件数：20个CSV文件

• 总记录数：16,000,020条

• 数据格式：逗号分隔值(CSV)

• 时间间隔：固定0.01的时间步长

• 数据完整性：100%（无缺失值）

数据优势

优势特征	具体表现	应用价值
数据规模庞大	1600万条记录，提供充足的训练数据	支持深度学习模型训练，避免过拟合
多样性丰富	20种不同类型的复杂函数，涵盖混沌、噪声、随机过程等	全面测试模型在不同场景下的泛化能力
数据质量高	100%完整性，无缺失值，固定时间步长	保证模型训练和评估的准确性和稳定性
复杂度高	包含高度非线性、混沌和随机特性	挑战现有预测模型，推动算法创新
实用性强	模拟真实世界中的复杂时间序列现象	研究成果可直接应用于实际问题

数据样例

以下是从不同类型数据集中选取的样本数据，展示了数据的多样性：

混沌系统样例（logistic_map.csv）

X,Y
0.00000,0.00000
0.01000,0.00037
0.02000,0.00074
0.03000,0.00111
0.04000,0.00148

随机过程样例（random_walk.csv）

X,Y
0.00000,0.00000
0.01000,-0.18324
0.02000,0.11412
0.03000,0.29038
0.04000,0.18149

混沌吸引子样例（lorenz_x_projection.csv）

X,Y
0.00000,1.00000
0.01000,1.00000
0.02000,1.02600
0.03000,1.07516
0.04000,1.14561

噪声过程样例（fractal_noise.csv）

X,Y
0.00000,0.0
0.01000,0.0017
0.02000,0.002
0.03000,0.00485
0.04000,0.00688

复杂周期函数样例（sum_of_two_sines.csv）

X,Y
0.00000,0.0
0.01000,0.0
0.02000,0.0
0.03000,0.00001
0.04000,0.00001

应用场景

1. 时间序列预测算法研究

本数据集为时间序列预测算法的研究提供了理想的测试平台。研究人员可以使用这些复杂的时间序列数据来开发和评估新的预测算法，特别是针对混沌系统和非线性过程的预测方法。通过在多样化的数据集上进行测试，可以更全面地评估算法的性能和泛化能力，推动时间序列预测领域的技术进步。

在这个应用场景中，研究人员可以：

• 比较传统方法（如ARIMA、Prophet）与深度学习方法（如LSTM、Transformer）在不同类型时间序列上的表现差异

• 探索针对特定类型数据（如混沌系统）的优化算法

• 研究特征工程和数据预处理技术对预测精度的影响

• 开发自适应模型，能够根据时间序列的特性自动调整参数

2. 机器学习模型鲁棒性测试

对于开发机器学习模型的工程师来说，本数据集是测试模型鲁棒性的宝贵资源。通过在具有不同复杂度和特性的时间序列上训练和测试模型，可以评估模型的泛化能力和对噪声、混沌和随机性的抵抗能力。这对于构建可靠的预测系统至关重要，尤其是在金融、医疗、能源等关键领域。

具体应用包括：

• 测试模型对极端值和异常点的敏感性

• 评估模型在非平稳数据上的表现

• 分析模型在不同信噪比条件下的预测精度

• 研究模型的长期预测能力和稳定性

3. 金融市场模拟与风险分析

金融市场的价格变动常常表现出混沌和随机特性，本数据集中的多种复杂函数可以用来模拟金融市场的动态行为。研究人员和金融分析师可以利用这些数据来测试交易策略、评估风险模型、研究市场微观结构等。特别是随机游走、分形噪声和混沌系统等数据类型，与金融时间序列的特性高度相似。

应用方式包括：

• 基于随机过程数据开发和测试交易算法

• 利用混沌系统研究市场的非线性动力学特性

• 使用分形噪声模拟市场的波动集群效应

• 构建蒙特卡洛模拟模型，评估投资组合的风险

4. 物理系统建模与仿真

本数据集包含多种物理系统的模拟数据，如Lorenz吸引子、Logistic映射等，可用于物理系统的建模与仿真研究。研究人员可以利用这些数据来开发新的控制算法、分析系统稳定性、研究混沌现象等。这对于理解复杂系统的行为特性、预测系统演化趋势具有重要意义。

相关应用包括：

• 基于混沌系统数据研究复杂系统的可预测性边界

• 开发针对非线性系统的控制策略

• 利用吸引子数据研究系统的相空间结构

• 分析系统参数对行为特性的影响

5. 信号处理与异常检测

本数据集中的多种时间序列类型，特别是包含噪声和异常模式的数据，为信号处理和异常检测算法的研究提供了良好的测试材料。研究人员可以利用这些数据来开发新的信号滤波技术、异常检测方法、特征提取算法等。这在工业监控、故障诊断、网络安全等领域具有重要应用价值。

具体应用包括：

• 开发针对复杂背景噪声的信号分离技术

• 研究基于时间序列特征的异常检测算法

• 构建自适应阈值模型，用于实时监控系统

• 利用分形特性分析信号的复杂性和不规则性

结尾

本数据集提供了丰富多样的复杂难预测时间序列数据，涵盖了混沌系统、分形噪声、随机过程等多种类型，总计超过1600万条记录。这些数据具有高度的复杂性和多样性，可以为时间序列预测、机器学习模型鲁棒性测试、金融市场模拟、物理系统建模和信号处理等研究提供有力支持。

数据集的主要价值在于其全面性和高质量，通过提供不同特性的时间序列数据，可以帮助研究人员开发出更强大、更鲁棒的预测算法和模型。这些算法和模型的进步将直接推动众多领域的技术创新和应用发展。

研究人员和工程师可以基于此数据集开展广泛的研究工作，探索时间序列预测的新方法和新技术，解决实际应用中的复杂问题。如有需要，可以进一步扩展数据集或开发特定领域的应用案例。